红黑树那点事儿
前置知识:二叉查找树、B树,本文不多做介绍。
0. 写在前面
在观察和思考红黑树时,一定要牢记:红黑树是一颗平衡二叉查找树,我们所赋予红黑树的一切行为,都是为了使其能够保持平衡性。
红黑树是由2-3-4树(4阶B树)等价过来的(当然也有由2-3树等价来的左倾或右倾红黑树),而这层等价关系,是我们用以维持红黑树平衡性的根本。
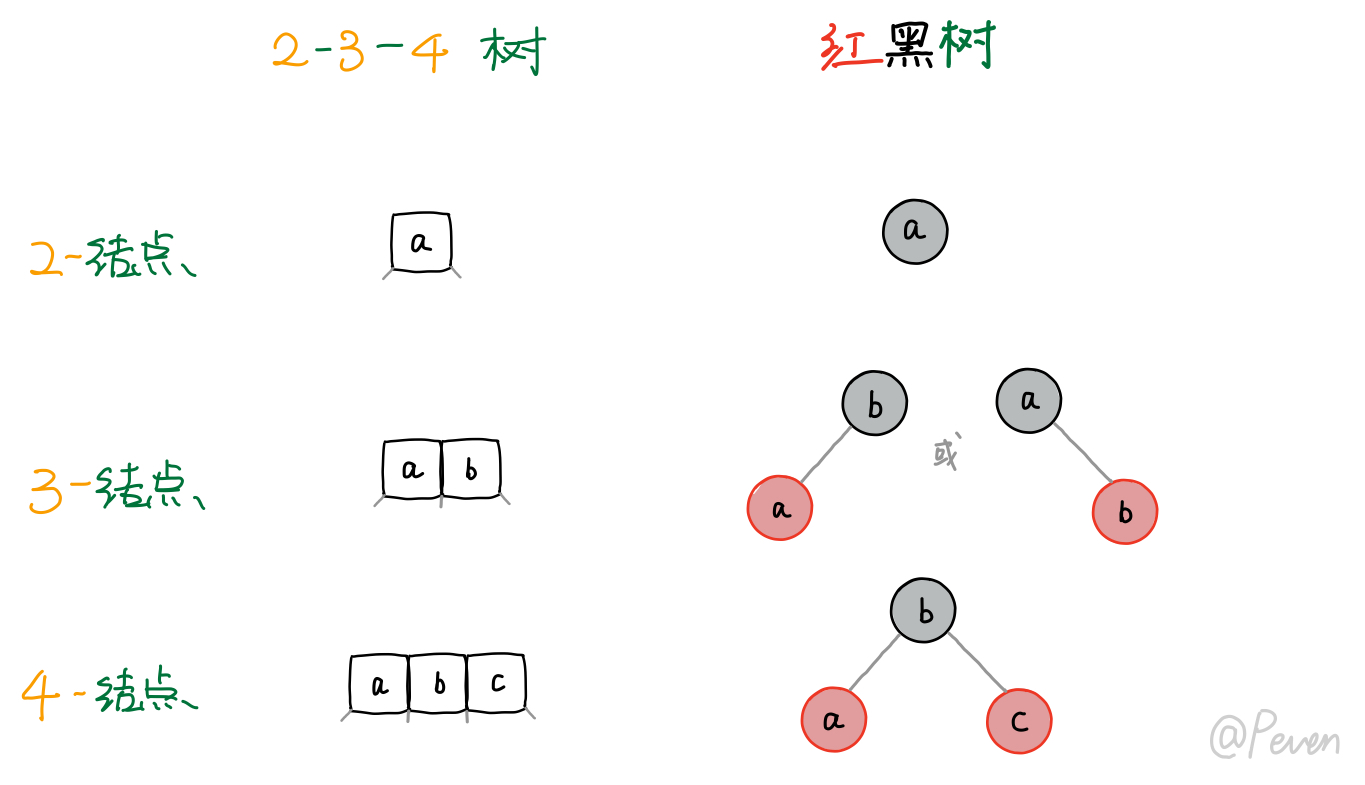
在红黑树中,我们以黑色来标识对应B树里的2-结点,而红色结点表示其parent到自己的链接是一条红链接(向上融合后对应B树中的3-结点,若兄弟结点也是红色则一起向上融合对应4-结点)
接下来我们来看看红黑树的五大性质:
- 结点为红色或黑色
- 根为黑色
- NULL叶子结点均为黑色
- 每个叶子结点到根的路径上不能有两个连续的红色结点
- 完美黑色平衡
通过前面展示的等价关系,要推导出这几条性质不成问题。
1. 旋转以及颜色翻转的本质
首先我们要明确一个概念:旋转是作用于红链接的操作。那么,旋转操作到底给我们的红黑树带来了怎样的影响呢?
Ⅰ. 旋转
旋转分为左旋(left-rotate)和右旋(right-rotate):
- 左旋:将右红链接转换为左红链接
- 右旋:将左红链接转换为右红链接
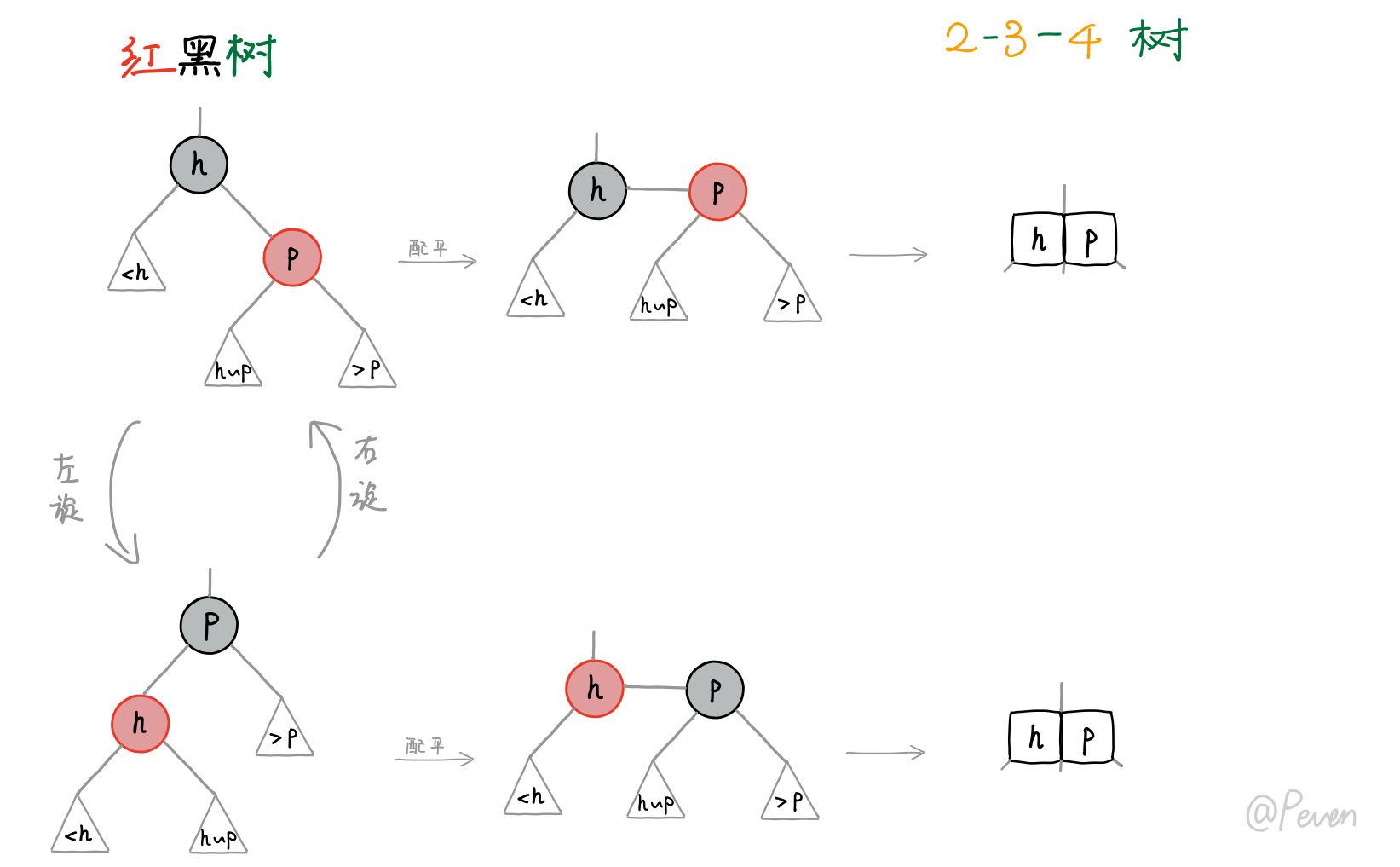
可以看到:在经过旋转操作后,我们可以调节某一侧黑色结点的平衡,而对应的2-3-4树结点并未发生任何变化。
Ⅱ. 颜色翻转(flip-color)
颜色翻转其实对应的是2-3-4树中4-结点需要分裂时的情况:一个新的KEY想要加入4-结点,会导致原有的4-结点分裂,原来中间的KEY会提到上层进行融合。
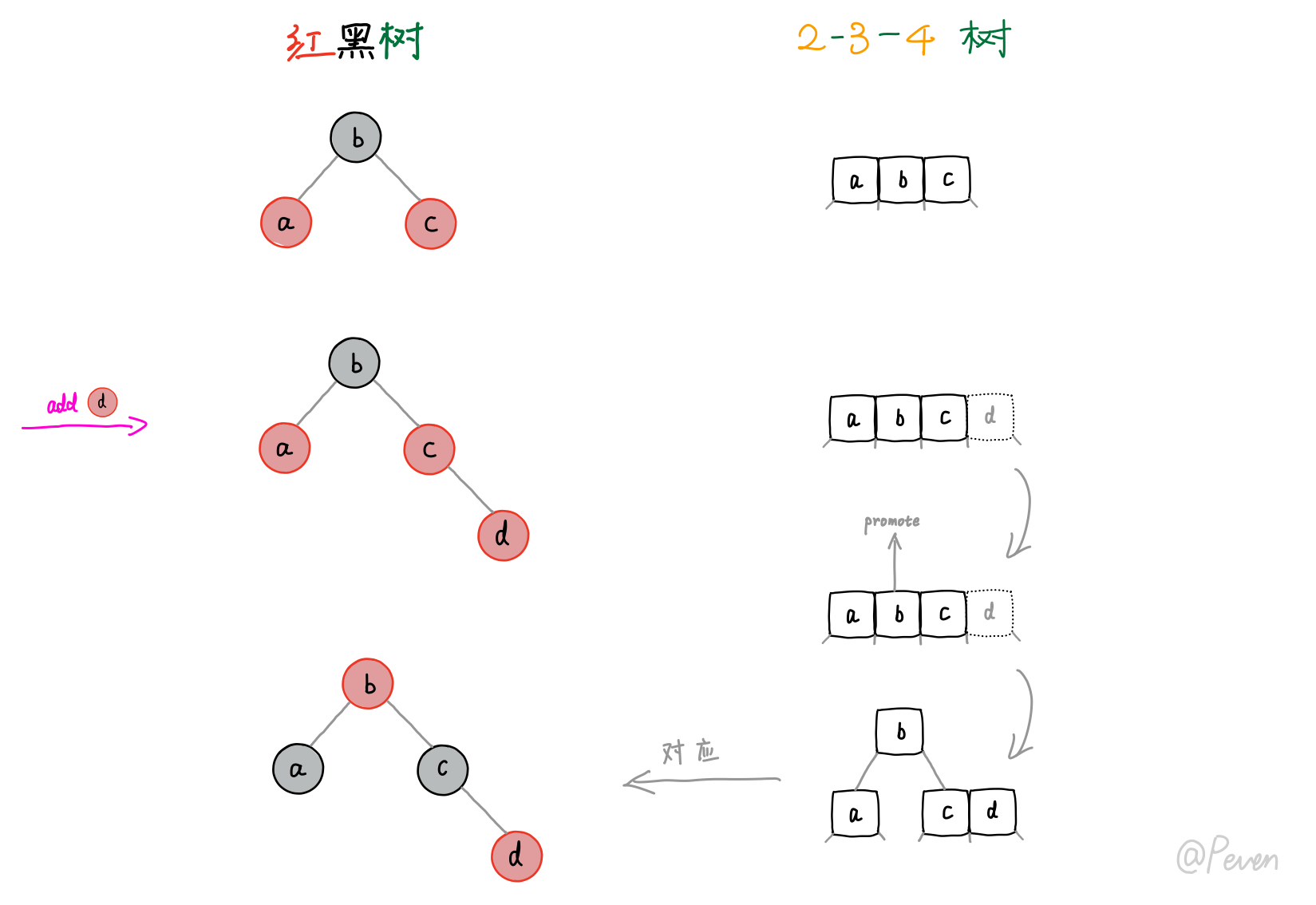
当我们插入d时,会形成一个临时5-结点,这时原先的4-结点将分裂,将b提上去进行融合(标为红色),当然,若此时b已经成为根节点,则进一步标为黑色。可以看到,我们通过简单的颜色翻转即可达到2-3-4树中结点分裂的效果。
2. 平衡性维持
在我们按照二叉查找树的规则做完插入或删除操作之后,就要通过观察对应2-3-4树中的变化,对我们的红黑树进行等价的操作从而恢复对应关系(即维持红黑树的平衡性)。
Ⅰ. 插入后的平衡性维持
新的结点作为红色叶子结点插入到树中,无非为以下4种情况:
a. 新增一个2-结点

如果新增的2-结点将作为根节点,则将其进一步标为黑色。
b. 与一个2-结点合并成为3-结点
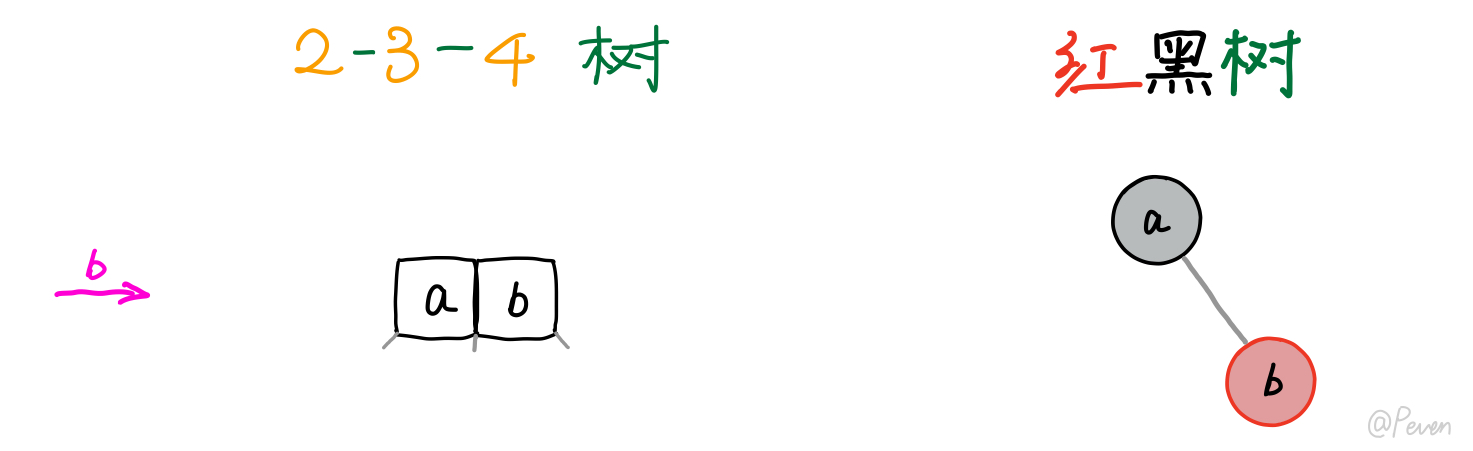
即新结点的parent结点为黑色,无需调整。
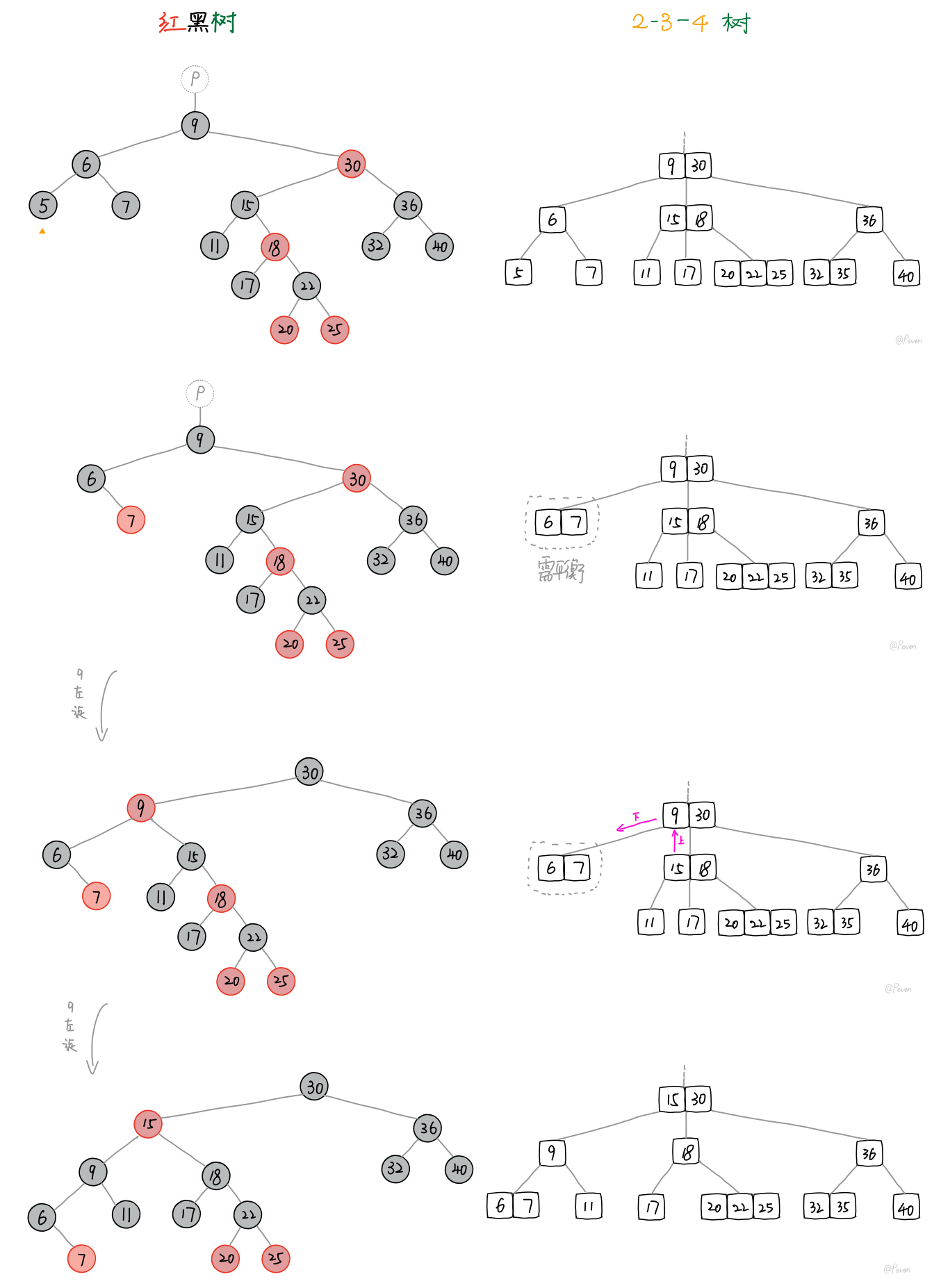
c. 与一个3-结点合并成为4-结点
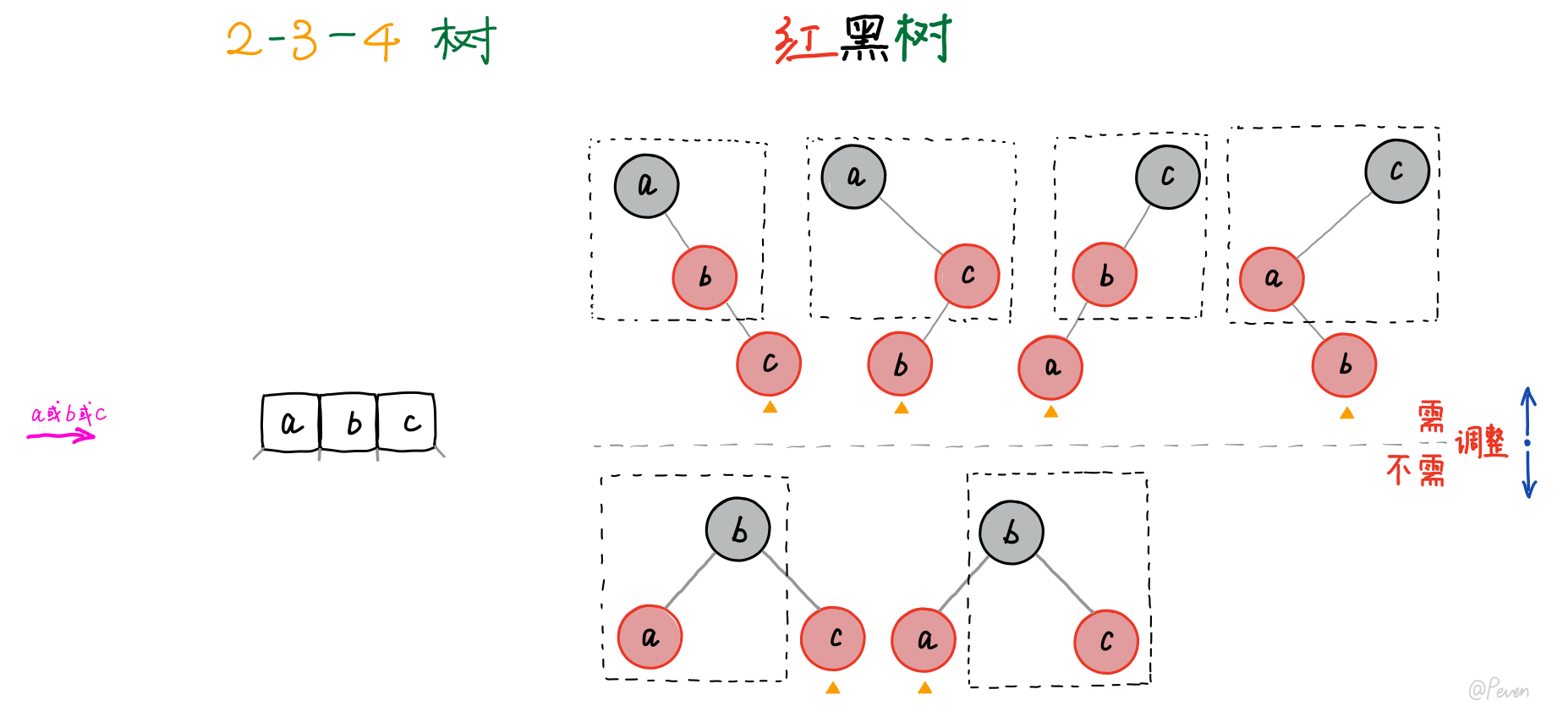
- 图中黑色虚线方框内是插入新节点时其
parent结点以及grandparent结点可能的情形 - 橙色三角标所指表示我们新插入的结点的位置
可能会出现连续两条红链接的情况,这时需要通过旋转操作进行调整(为上图下半部分的形式)。
d. 与一个4-结点进行合并, 4-结点需要分裂(颜色翻转)
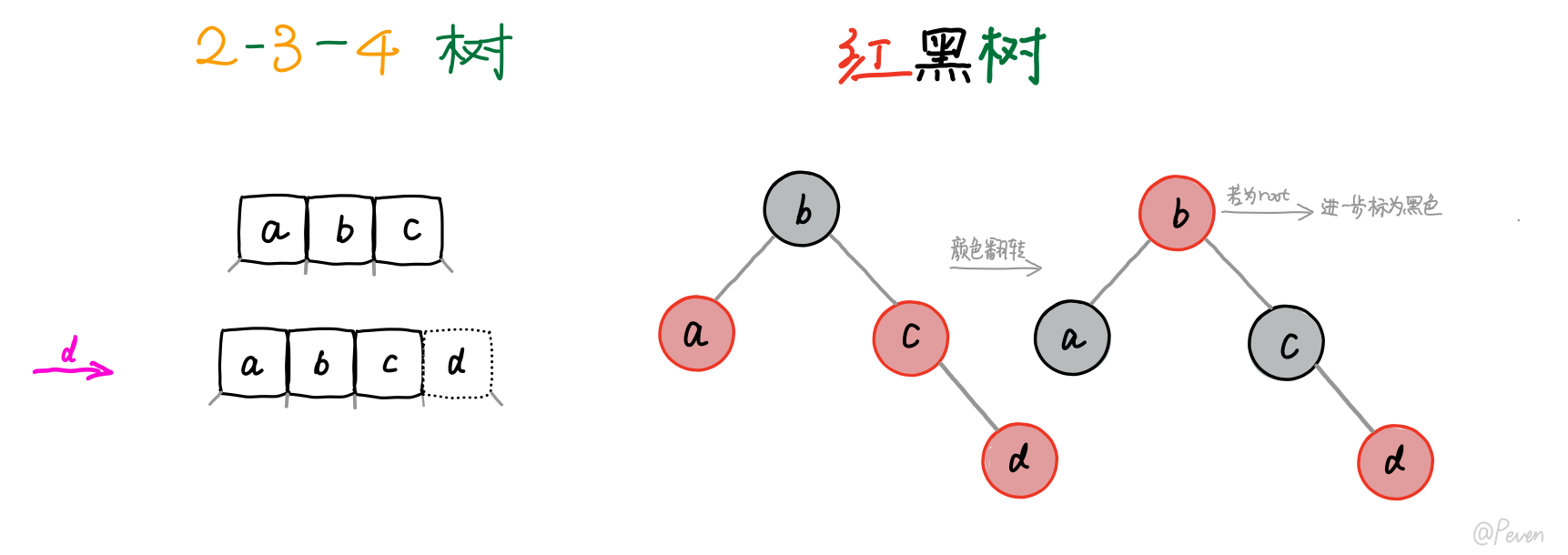
Ⅱ. 删除后的平衡性维持
删除操作同BST大体相同,不过在我们的代码实现里,被删除的永远是一个替代结点。因为红黑树由2-3-4树等价而来,我们要充分对其性质进行利用。
那么替代结点究竟如何得到呢?我们先查找到指定删除的结点d,如果该结点有两个孩子,则替代结点为其前驱或后继结点;如果该结点只有一个孩子,该孩子就是替代结点;若d没有孩子(即d为根结点),则替代结点就是其本身。
因为2-3-4树的完美平衡性质,我们可以得到一个结论:真正被删除的元素一定是2-3-4树中的叶子节点中的KEY,也即在红黑树中删除的(替代结点)一定是叶子节点或者叶子结点上面的双亲结点(最多只有一个孩子)。
进一步得出以下推论:若替代结点的左孩子不为空,则替代结点一定是一个前驱结点;反之,是一个后继结点。删除后用其子节点替代自己的位置。
而这又对应了2-3-4树中叶子结点的状况:
2-结点:删除后兄弟够借,经过双亲借;兄弟不够,啃老来凑- 非
2-结点:自己足够,直接删除
而后我们的删除策略就变成了(以用前驱结点替代为例):
- 若删除的替代结点有孩子,且替代结点为黑色,将孩子变为黑色来替代自己
- 删除的是一个叶子节点,且这个替代结点为黑色,在删除前先进行平衡修复(避免提前删除导致信息丢失)
接下来讨论上述第二种情况:需要平衡修复的情况。
a. 兄弟够借
向兄弟结点借之前得先知道兄弟手里够不够吧,所以需要找到真正的兄弟结点,因为若当前替代结点的兄弟是红色结点的话,对应2-3-4树,在红黑树中根本不是真正的兄弟结点。如下图第二种情况(图中p表示parent结点哦):
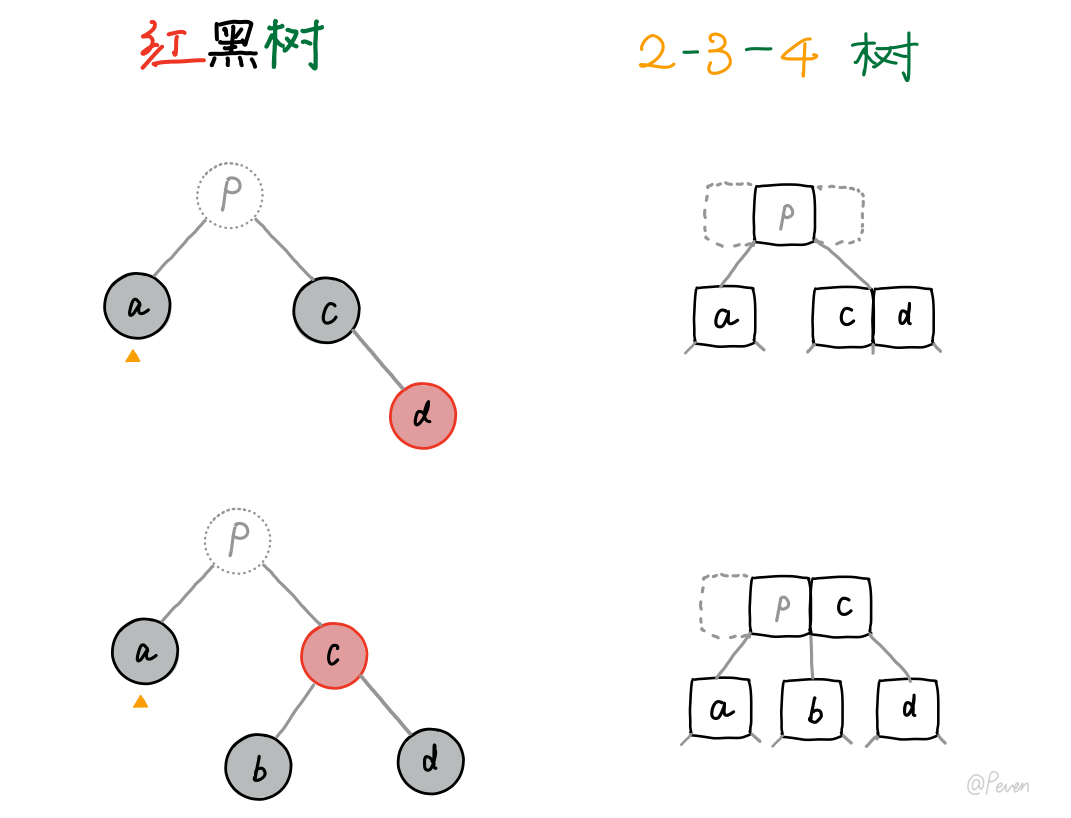
这时我们只需对替代结点的parent结点做一次旋转操作即可(出现红链接了),如下所示:
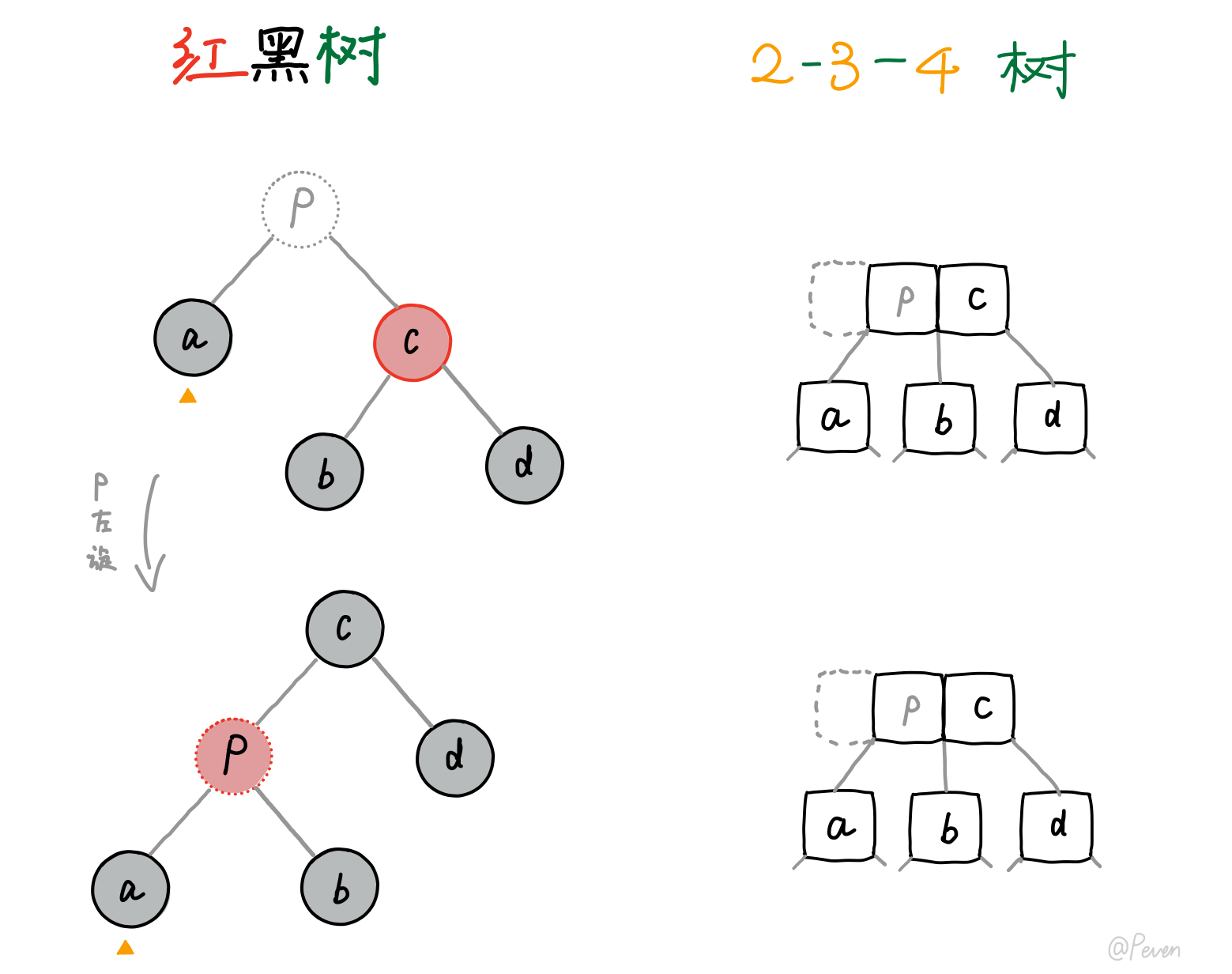
找到真正的兄弟结点之后,如果兄弟结点的孩子中有红色结点,就对应了2-3-4树中非2-结点可借的情况。
既然兄弟够借,那么对应2-3-4树中,就是兄弟中KEY最接近自己的上去顶替parent,parent下来顶替被删的结点。
为了实现起来简单,这里有一个小trick:通过旋转将兄弟与兄弟孩子结点达到某种关系后,再旋转parent结点。这样做可以达到在对应2-3-4树中如果有兄弟有两个孩子就从兄弟那里借两个来的效果,而且可以大大的简化我们的代码。
例如被删结点是其parent的左孩子,找到其真正的右兄弟后,如果右兄弟有两个红色子节点,直接旋转parent,这样,兄弟结点中只会留下右孩子(较大的KEY),兄弟结点上升代替parent,parent与兄弟左孩子下来代替删除的结点,左孩子没有的话也没关系;另一种需要提前调整的情况是,右兄弟只有一个左孩子可借,这时候我们对右兄弟进行右旋后再对parent进行左旋即可。
然而我们前面说:旋转操作是针对红链接的。然而我们在这里其实很幸运地跳出了这个规则的束缚,只需做小许额外的步骤:
对
parent旋转之后, 兄弟顶上去替代parent的位置, 兄弟被染成了parent原来的颜色 —— 上去顶替,没毛病但
parent变成了红色,不过因为parent是下来顶替被删的黑色结点,故需将其染成黑色最后,将兄弟结点之前的右孩子标为黑色 —— 只剩下它了,作为一个
2-结点
若被删结点是其parent的右孩子,把上面的逻辑反过来左右对调即可。
如果真兄弟结点的两个孩子均为黑色,就对应了2-结点、不可借的情况,我们将在下面继续进行讨论。
b. 兄弟不够
兄弟无法借过来,对应2-3-4树中,兄弟就得找parent合并。所以直接将兄弟结点变成红色,交由上层解决。若parent也是红色,就把parent变成黑色。若parent本身就是黑色,就得让parent再找他自己的兄弟结点借。
3. 代码实现
1package rbt
2
3const (
4 RED = true
5 BLACK = false
6)
7
8type (
9 // KeyType is the type with CompareTo behavior.
10 KeyType interface {
11 CompareTo(c interface{}) int
12 }
13
14 // KeyTypeInt is the int that implements the KeyType interface.
15 KeyTypeInt int
16
17 // node is the red-black tree node
18 node struct {
19 Key KeyType
20 Val interface{}
21 Color bool
22 Left *node
23 Right *node
24 Parent *node
25 }
26
27 // RBT is the red-black tree
28 RBT struct {
29 root *node
30 size int
31 }
32)
33
34// CompareTo implementation for type KeyTypeInt
35func (k KeyTypeInt) CompareTo(c interface{}) int {
36 return int(k) - int(c.(KeyTypeInt))
37}
38
39// isRed returns whether a node is in red color, nil is black
40func isRed(n *node) bool {
41 if n == nil {
42 return BLACK
43 }
44 return n.Color
45}
46
47// NewRBT returns a red-black tree
48func NewRBT() *RBT {
49 return &RBT{}
50}
51
52// treeMin find the minimum node in n's sub-tree
53// func (n *node) treeMin() *node {
54// for n.Left != nil {
55// n = n.Left
56// }
57// return n
58// }
59
60// treeMax find the maximum node in n's sub-tree
61func (n *node) treeMax() *node {
62 for n.Right != nil {
63 n = n.Right
64 }
65 return n
66}
67
68// predecessor returns n's predecessor node
69func (n *node) predecessor() *node {
70 if n == nil {
71 return nil
72 }
73
74 if n.Left != nil {
75 return n.Left.treeMax()
76 } else {
77 p := n.Parent
78 lc := n
79 for p != nil && lc == p.Left {
80 lc = p
81 p = p.Parent
82 }
83 return p
84 }
85}
86
87// successor returns n's successor node
88// func (n *node) successor() *node {
89// if n == nil {
90// return nil
91// }
92
93// if n.Right != nil {
94// return n.Right.treeMin()
95// } else {
96// p := n.Parent
97// lc := n
98// for p != nil && lc == p.Right {
99// lc = p
100// p = p.Parent
101// }
102// return p
103// }
104// }
105
106// LeftRotate left rotate the node n, acting on a red link
107//
108// p p
109// | |
110// n m
111// / \ / \
112// nl m ==> n mr
113// / \ / \
114// ml mr nl ml
115//
116func (t *RBT) leftRotate(n *node) {
117 m := n.Right
118 n.Right = m.Left
119 if m.Left != nil {
120 m.Left.Parent = n
121 }
122 m.Parent = n.Parent
123 if n.Parent == nil {
124 t.root = m
125 } else if n == n.Parent.Left {
126 n.Parent.Left = m
127 } else {
128 n.Parent.Right = m
129 }
130 m.Left = n
131 n.Parent = m
132 // repaint color
133 m.Color = n.Color
134 n.Color = RED
135}
136
137// RightRotate right rotate the node n, acting on a red link
138//
139// p p
140// | |
141// n m
142// / \ / \
143// m nr ==> ml n
144// / \ / \
145// ml mr mr nr
146//
147func (t *RBT) rightRotate(n *node) {
148 m := n.Left
149 n.Left = m.Right
150 if m.Right != nil {
151 m.Right.Parent = n
152 }
153 m.Parent = n.Parent
154 if n.Parent == nil {
155 t.root = m
156 } else if n == n.Parent.Left {
157 n.Parent.Left = m
158 } else {
159 n.Parent.Right = m
160 }
161
162 m.Right = n
163 n.Parent = m
164 // repaint color
165 m.Color = n.Color
166 n.Color = RED
167}
168
169func (t *RBT) flipColors(n *node) {
170 n.Color = RED
171 n.Left.Color = BLACK
172 n.Right.Color = BLACK
173}
174
175// Search returns the node by the given key if it exists
176func (t *RBT) Search(key KeyType) *node {
177 root := t.root
178 for root != nil {
179 cmp := key.CompareTo(root.Key)
180 if cmp < 0 {
181 root = root.Left
182 } else if cmp > 0 {
183 root = root.Right
184 } else {
185 return root
186 }
187 }
188 return root
189}
190
191// Insert inserts a key with associated data(val) to a place in the red-black
192// tree by compare the keys, and if the key exists, update it with the new val.
193func (t *RBT) Insert(key KeyType, val interface{}) {
194 if t.root == nil {
195 t.root = &node{Key: key, Val: val}
196 t.size = 1
197 return
198 }
199
200 // find parent node to attach
201 root := t.root
202 var p *node
203 for root != nil {
204 p = root
205 cmp := key.CompareTo(root.Key)
206 if cmp < 0 {
207 root = root.Left
208 } else if cmp > 0 {
209 root = root.Right
210 } else {
211 root.Val = val
212 return
213 }
214 }
215
216 newnode := &node{Key: key,
217 Val: val,
218 Color: RED,
219 Parent: p,
220 }
221
222 cmp := key.CompareTo(p.Key)
223 if cmp < 0 {
224 p.Left = newnode
225 } else {
226 p.Right = newnode
227 }
228
229 t.insertFix(newnode)
230 t.size++
231}
232
233func (t *RBT) insertFix(n *node) {
234 var u *node // n's uncle node
235 for n.Parent != nil && isRed(n.Parent) {
236 if n.Parent == n.Parent.Parent.Left {
237 u = n.Parent.Parent.Right
238 if u != nil && isRed(u) {
239 n = n.Parent.Parent
240 t.flipColors(n)
241 } else {
242 if n == n.Parent.Right {
243 n = n.Parent
244 t.leftRotate(n)
245 }
246 t.rightRotate(n.Parent.Parent)
247 }
248 } else {
249 u = n.Parent.Parent.Left
250 if u != nil && isRed(u) {
251 n = n.Parent.Parent
252 t.flipColors(n)
253 } else {
254 if n == n.Parent.Left {
255 n = n.Parent
256 t.rightRotate(n)
257 }
258 t.leftRotate(n.Parent.Parent)
259 }
260 }
261 }
262 // root should be black node at the end
263 t.root.Color = BLACK
264}
265
266// Remove delete a node by the given key if it exits
267func (t *RBT) Remove(key KeyType) {
268 d := t.Search(key)
269
270 if d == nil {
271 return // not found
272 }
273
274 // find replacement node
275 // in our code, if finally the rpl hold a child node, the rpl must be a
276 // predecessor or successor
277 rpl := d
278 if rpl.Left != nil && rpl.Right != nil {
279 // rpl = rpl.successor()
280 rpl = rpl.predecessor()
281 } else {
282 if rpl.Left != nil {
283 rpl = rpl.Left
284 } else if rpl.Right != nil {
285 rpl = rpl.Right
286 }
287 }
288 // delete replacement node
289 if rpl != t.root {
290 if d != rpl { // d is not a leaf node
291 d.Key = rpl.Key
292 d.Val = rpl.Val
293 }
294
295 if rpl.Left != nil { // rpl is a predecessor
296 if !isRed(rpl) {
297 rpl.Left.Color = BLACK
298 }
299
300 rpl.Left.Parent = rpl.Parent
301 if rpl == rpl.Parent.Left {
302 rpl.Parent.Left = rpl.Left
303 } else {
304 rpl.Parent.Right = rpl.Left
305 }
306 // unlink rpl
307 rpl.Parent = nil
308 rpl.Left = nil
309 } else {
310 // rpl is a leaf node
311 // fix
312 if !isRed(rpl) {
313 t.removeFix(rpl)
314 }
315 // then delete
316 if rpl == rpl.Parent.Left {
317 rpl.Parent.Left = nil
318 } else {
319 rpl.Parent.Right = nil
320 }
321 // unlink rpl
322 rpl.Parent = nil
323 }
324 } else { // single node tree
325 t.root = nil
326 }
327 t.size--
328}
329
330// fixAfterRemove do fix if the deleted node is in black color
331func (t *RBT) removeFix(n *node) {
332 for n != t.root && !isRed(n) {
333 if n == n.Parent.Left {
334 rBro := n.Parent.Right
335 // find real brother node
336 if isRed(rBro) {
337 t.leftRotate(n.Parent)
338 rBro = n.Parent.Right
339 }
340 if !isRed(rBro.Left) && !isRed(rBro.Right) { // can't borrow
341 rBro.Color = RED
342 n = n.Parent
343 } else { // can borrow
344 // 3-node
345 if !isRed(rBro.Right) {
346 t.rightRotate(rBro)
347 rBro = n.Parent.Right
348 }
349 t.leftRotate(n.Parent)
350 // since we pull down n's parent to replace n and
351 // we borrow two n's bro's childern, we need repaint
352 n.Parent.Color = BLACK
353 rBro.Right.Color = BLACK
354 n = t.root
355 }
356 } else {
357 lBro := n.Parent.Left
358
359 if isRed(lBro) {
360 t.rightRotate(n.Parent)
361 lBro = n.Parent.Left
362 }
363 if !isRed(lBro.Left) && !isRed(lBro.Right) {
364 lBro.Color = RED
365 n = n.Parent
366 } else {
367 if !isRed(lBro.Left) {
368 t.leftRotate(lBro)
369 lBro = n.Parent.Left
370 }
371 t.rightRotate(n.Parent)
372 n.Parent.Color = BLACK
373 lBro.Left.Color = BLACK
374 n = t.root
375 }
376 }
377 }
378 n.Color = BLACK
379}
4. Do something fun:红黑树可视化
用graphviz库(需自行安装dot工具包)给我们的红黑树实现了Visualize方法:
1func (t *RBT) Visualize() {
2 G := visuzlizeTree(t.root)
3 G.GenerateImage("dot", "rbt.svg", "svg")
4}
5
6func visuzlizeTree(root *node) *graphviz.Graph {
7 G := &graphviz.Graph{}
8 addSubTree(root, G)
9 G.DefaultNodeAttribute(graphviz.Shape, graphviz.ShapeCircle)
10 G.DefaultNodeAttribute(graphviz.FontName, "JetBrainsMono Nerd Font")
11 G.GraphAttribute(graphviz.NodeSep, "0.3")
12 G.DefaultNodeAttribute(graphviz.Style, graphviz.StyleFilled)
13 G.DefaultNodeAttribute(graphviz.FillColor, "#B7BBBC")
14 // G.MakeDirected()
15 return G
16}
17
18func addSubTree(root *node, G *graphviz.Graph) int {
19 if root == nil {
20 null := G.AddNode("")
21 G.NodeAttribute(null, graphviz.Shape, graphviz.ShapePoint)
22 return null
23 }
24 rootnode := G.AddNode(fmt.Sprint(root.Key))
25 if root.isRed() {
26 G.NodeAttribute(rootnode, graphviz.Style, graphviz.StyleFilled)
27 G.NodeAttribute(rootnode, graphviz.FillColor, "#F8BCC2")
28 }
29 leftnode := addSubTree(root.Left, G)
30 rightnode := addSubTree(root.Right, G)
31 G.AddEdge(rootnode, leftnode, "")
32 G.AddEdge(rootnode, rightnode, "")
33 return rootnode
34}
调用生成rbt.svg:
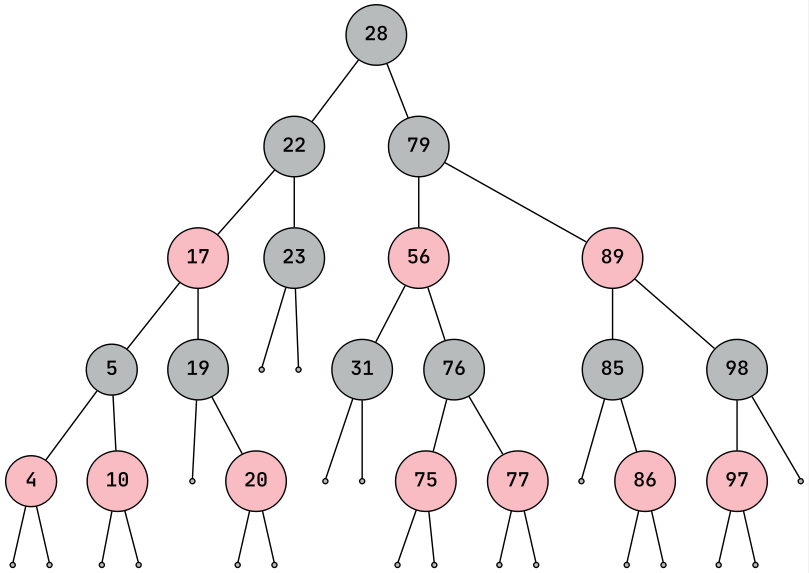
5. 总结
本文沿着红黑树同2-3-4树的关系脉络来讨论了红黑树里的插入及删除操作,其可能涉及的情况十分繁多,本文亦不能做到面面俱到。手绘的图也只展示了部分情况,力图通过简单的梳理来理解红黑树平衡性的本质。假如如果你此前对于B树已有很深入的理解的话,相信理解红黑树也不会花费太多时间。
